Fractals are awesome. Fractals are EVERYWHERE in your life - but what the eff IS a fractal? I decided to consult the all-knowing Wikipedia and a fractal is defined as a
mathematical set that has a fractal dimension that usually exceeds its topological dimension[1] and may fall between the integers.[2] Fractals are typically self-similar patterns, where self-similar means they are "the same from near as from far"[3] Fractals may be exactly the same at every scale [or] they may be nearly the same at different scales.
That’s all fine and good, but what does that mean? What does a fractal look like? Why do fractals matter?
What does a fractal look like?
Imagine a tree. Starting with the base of the trunk you have a thick stick coming out of the ground. This ‘stick’ then splits into smaller branches -
 branches that look very very similar to the original ‘stick.’ From there, each smaller branch splits into even smaller, very similar branches and so forth to form the complete tree. This is a ‘natural’ fractal - one that appears in nature EVERYWHERE on earth.
branches that look very very similar to the original ‘stick.’ From there, each smaller branch splits into even smaller, very similar branches and so forth to form the complete tree. This is a ‘natural’ fractal - one that appears in nature EVERYWHERE on earth.
You also have the example of river deltas and other flowing bodies for liquid, where each new path the liquid takes creates an nearly identical and to scale replica of the larger formation itself:
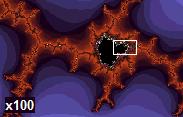
There are also fractals that can be simulated using computers and mathematical formulas, of which I have no understanding in even the most basic aspect. The images they create, however are incredibly beautiful, with a strange almost ghostly implied symmetry as you change the scale (zoom in or out infinitely, theoretically). The most famous, and iconic of these simulated fractals is the Mandelbrot Set, discovered and described by French-American mathematician, Benoit Mandelbrot (1924-2010).
What the exploitation of fractals allowed was a calculation of the dimensionality of the curving coastline, to calculate the actual length. Again, much of this goes over my head, but from what I understand a coastline can be measured using any number between (or including) 1 or 2. The West Coast of Britain, as an example has a calculated dimension of 1.25 (and that's a jagged coast). While I couldn’t find if the measurement was ever made, the wonder of fractals made it a possibility.
Further reading and sources:
http://en.wikipedia.org/wiki/Fractal
http://en.wikipedia.org/wiki/How_Long_Is_the_Coast_of_Britain%3F_Statistical_Self-Similarity_and_Fractional_Dimension
http://www.glyphs.com/art/fractals/what_is.html
Pretty Picture of fractals:
http://www.enchgallery.com/fractals/fracthumbs.htm
http://sprott.physics.wisc.edu/fractals.htm
There are also fractals that can be simulated using computers and mathematical formulas, of which I have no understanding in even the most basic aspect. The images they create, however are incredibly beautiful, with a strange almost ghostly implied symmetry as you change the scale (zoom in or out infinitely, theoretically). The most famous, and iconic of these simulated fractals is the Mandelbrot Set, discovered and described by French-American mathematician, Benoit Mandelbrot (1924-2010).
Starting at the x1 magnification and increasing up to x2000, the patterns are self similar, the patterns are the same near or far!
Why do fractals matter?
By using smaller and smaller measuring devices, you are able to measure finer and finer number of natural curves in the coastline itself.
Why do fractals matter?
While fractals were first described as early of the 17th Century, the first real practical use and description was provided by the previously mentioned Mandelbrot. His usage? Measuring the length of Great Britain’s coastline! I know it seems like a piece of information we should have had for awhile, it was discussed in the 1967 paper by Mandelbrot titled “How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension.”
The main issue with measuring the coast line is what had been known as the coastline paradox. This paradox explains that as you measure a coastline, the total length of the coastline increases without limit as the too used to measure the distance get’s smaller. In English: if you measured a coastline with a yard stick and then a stand 12-inch ruler, the ruler would return a LARGER length of coastline than the yard stick.By using smaller and smaller measuring devices, you are able to measure finer and finer number of natural curves in the coastline itself.
Using a yardstick may result in this type of measurement:
Using the ruler may (not to scale, of course) result in something more like this:
What the exploitation of fractals allowed was a calculation of the dimensionality of the curving coastline, to calculate the actual length. Again, much of this goes over my head, but from what I understand a coastline can be measured using any number between (or including) 1 or 2. The West Coast of Britain, as an example has a calculated dimension of 1.25 (and that's a jagged coast). While I couldn’t find if the measurement was ever made, the wonder of fractals made it a possibility.
Further reading and sources:
http://en.wikipedia.org/wiki/Fractal
http://en.wikipedia.org/wiki/How_Long_Is_the_Coast_of_Britain%3F_Statistical_Self-Similarity_and_Fractional_Dimension
http://www.glyphs.com/art/fractals/what_is.html
Pretty Picture of fractals:
http://www.enchgallery.com/fractals/fracthumbs.htm
http://sprott.physics.wisc.edu/fractals.htm






No comments:
Post a Comment